Из вершины А треугольника АВС проведён отрезок АК, перпендикулярный плоскости...

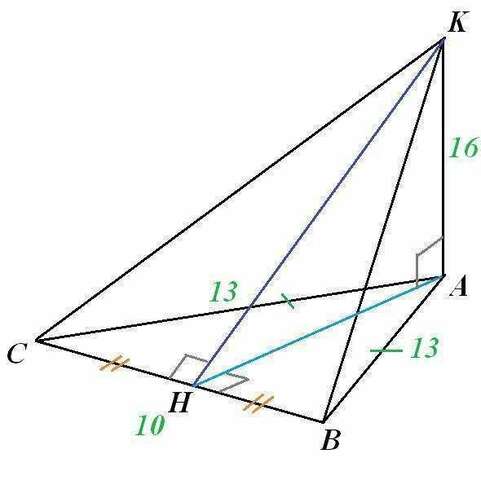
Т.к. КА по условию перпендикуляр, то КС и КВ - наклонные, АС и АВ соответственно их проекции на плоскость АВС.
По условию АС=АВ, значит, ΔАВС - равнобедренный с основанием СВ.
Т.к. проекции равны (АС=АВ), то равны сами наклонные, т.е. КС=КВ, и ΔВСК - равнобедренный с основанием СВ.
Проведем в ΔВСК высоту КН. Тогда $S_{\DeltaBCK}= \frac{1}{2} KH*CB$
КН также является наклонной для перпендикуляра АК, АН - ее проекция на плоскость АВС.
По теореме, обратной теореме о трех перпендикулярах, АН⊥СВ. Значит, АН является высотой, следовательно, и медианой в ΔАВС.
Отсюда, СН=ВН=5.
В ΔАВН по теореме Пифагора АН²=АВ²-ВН²
$AH= \sqrt{13^2-5^2} = \sqrt{8*18} = \sqrt{16*9}=4*3=12$
В ΔКАН по теореме Пифагора КН²=АН²+АК²
$KH= \sqrt{12^2+16^2} = \sqrt{400} = 20$
Наконец, $S_{\DeltaBCK}= \frac{1}{2} *20*10=100$
Ответ: 100.