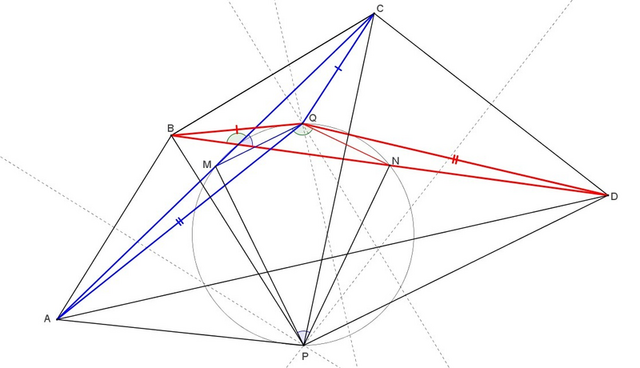
Треугольники AQC и DQB очевидно равны по трем сторонам, а значит совмещаются поворотом вокруг точки Q (синий и красный треугольники). Значит их медианы QN и QM тоже совместятся при этом повороте, т.е. ∠MQN равен углу между прямыми AC и DB (т.к. диагональ AC переходит в DB).
Аналогично, треугольники APC и BPD совместятся поворотом вокруг точки Р, т.е., ∠MPN между их медианами РМ и РN тоже равен углу между диагоналями четырехугольника. В любом случае, получаем либо ∠MPN=∠MQN, либо ∠MPN+∠MQN=180°, что и означает, что точки PQМN лежат на одной окружности.