Площадь трапеции равна произведению полусуммы оснований на высоту.
а)Если в равнобедренной трапеции диагонали перпендикулярны, то её высота равна средней линии.
Средняя линия трапеции, как известно, равна полусумме оснований.
(a+b):2=H=14
S=14²=196 (ед. площади)
б)Диагонали равнобедренной трапеции равны.
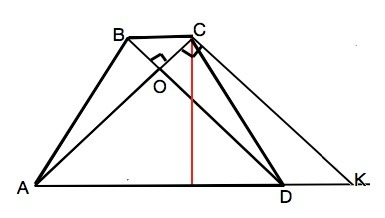
Проведем из С параллельно BD прямую до пересечения с продолжением АD в точке К.
Противолежащие стороны четырехугольника ВСКD параллельны, ⇒
DК=BC.
АK=AD+BC
Угол АСК=углу АОD=90°
В ∆ АСК AC=CK, ⇒∆ АСК прямоугольный равнобедренный,
АН=НК=СН=14
Площадь АСК=СН•AК:2=14•14=196
Площадь трапеции СН•(АD+BC):2=СН•АК:2=196
------
Такой способ нахождения площади трапеции можно применять, когда известны длины оснований и диагоналей. Площадь трапеции равна площади треугольника АСК которую можно вычислить по ф. Герона.