Величина угла между плоскостями – угол, сторонами которого являются лучи, по которым эти плоскости пересекаются плоскостью, перпендикулярной ребру угла.
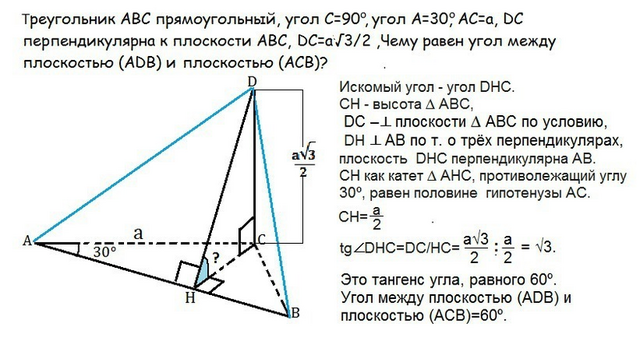
Искомый угол –это угол DHC, образованный отрезками СН и DH (см. рисунок в приложении).
СН - высота ∆ АВС, DC –⊥ плоскости ∆ АВС по условию, DH ⊥ АВ по т. о трёх перпендикулярах,
плоскость DHC перпендикулярна АВ.
СН как катет ∆ АНС, противолежащий углу 30º, равен половине гипотенузы АС и равен а/2
Тангенс угла DHC=DC/HC=[(а√3):2]:a/2=√3.
Это тангенс угла, равного 60º.
Угол между плоскостью (ADB) и плоскостью (ACB)=60º.