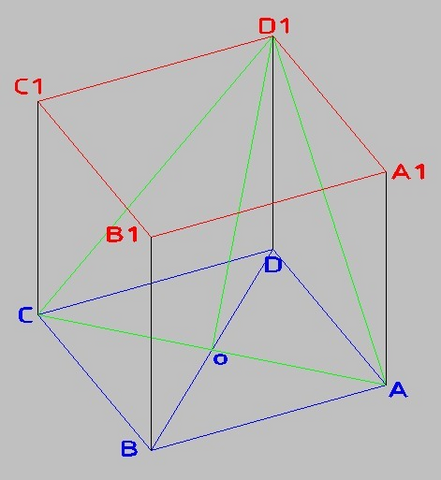
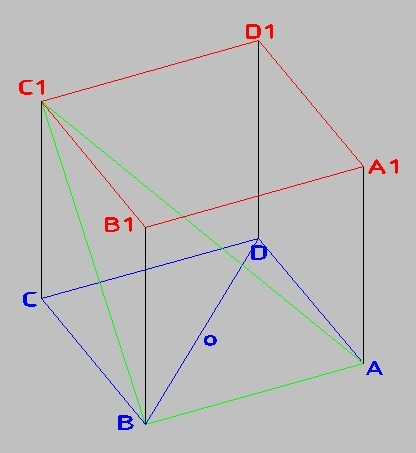
На рисунках низ синий, верх красный, рассматриваемые сечения-диагонали - зелёные.
1) займёмся сечением ACD₁
Пусть ребро куба х
Тогда диагональ грани AC по Пифагору
AC² = x²+x²
AC = x√2
OD - половина диагонали грани
OD = 1/2*AC = x/√2
И снова по Пифагору гипотенуза OD₁ треугольника ODD₁
OD₁² = OD²+DD₁²
OD₁² = x²/2+x² = 3/2*x²
OD₁ = x√(3/2)
Площадь сечения ACD₁
S(ACD₁) = 1/2*AC*OD₁ = 1/2*x√2*x√(3/2) = x²√3/2
И по условию
S(ACD₁) = 25/2*√3 см²
x²√3/2 = 25/2*√3
x² = 25
x = 5 см
2) Объёмная диагональ куба
BD₁² = 3x²
BD₁ = x√3 = 5√3 см
3) Сечение АВС₁
Прямая ВС₁ перпендикулярна АВ, т.к. она лежит в плоскости, перпендикулярной АВ
S(АВС₁) = 1/2*АВ*ВС₁ = 1/2*x*x√2 = 25/√2 см