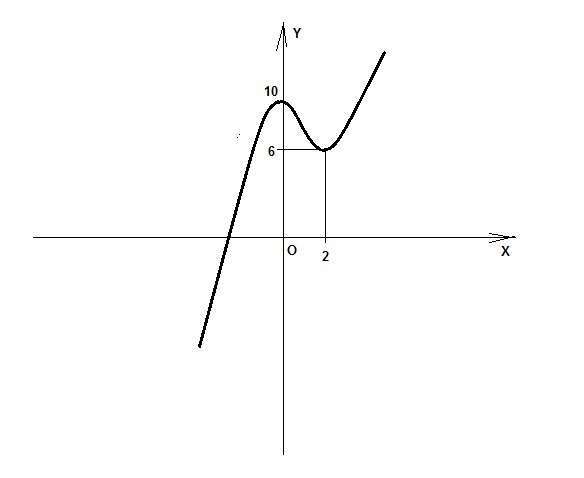
10) y = x^3 - 3x^2 + 10
План исследования функции:
1) Область определения: x ∈ (-oo; +oo)
2) Область значений: y ∈ (-oo; +oo)
3) Пересечение с осями
Пересечение с осью Oy: y(0) = 10
y = 0 трудно найти, y(-1) = -1-3+10 = 6 > 0; y(-2) = -8-12+10 = -10 < 0
Пересечение с осью Ox на промежутке (-2; -1)
4) Разрывов нет, функция всюду непрерывна.
5) Экстремумы. y ' = 0
y ' = 3x^2 - 6x = 3x(x - 2) = 0
x1 = 0; y1 = 10 - максимум
x2 = 2; y2 = 8 - 3*4 + 10 = 6 - минимум
При x ∈ (-oo; 0) будет y' > 0, функция возрастает
При x ∈ (0; 2) будет y' < 0, функция убывает
При x ∈ (2; +oo) будет y' > 0, функция возрастает.
6) Точки перегиба. y '' = 0
y '' = 6x - 6 = 0
x = 1; y(1) = 1 - 3 + 10 = 8
При x ∈ (-oo; 1) будет y'' < 0, функция выпуклая вверх
При x ∈ (1; +oo) будет y'' > 0, функция выпуклая вниз.
7) Наклонные и горизонтальные асимптоты.
Возможная наклонная имеет уравнение f(x) = kx + b, где:

Асимптот нет.
График примерно нарисован.