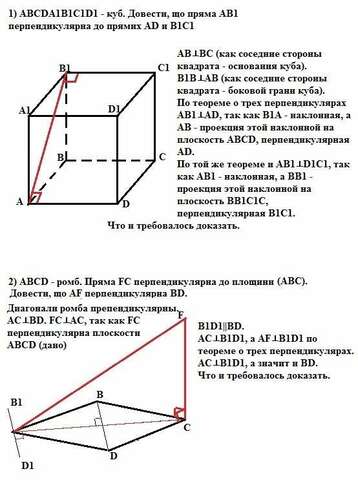
1) АВ⊥ВС (как соседние стороны квадрата - основания куба).
В1В⊥АВ (как соседние стороны квадрата - боковой грани куба).
По теореме о трех перпендикулярах АВ1⊥AD, так как В1А - наклонная, а АВ - проекция этой наклонной на плоскость АВСD, перпендикулярная AD.
По той же теореме и АВ1⊥D1C1, так как АВ1 - наклонная, а ВВ1 - проекция этой наклонной на плоскость ВВ1С1C, перпендикулярная В1С1.
Что и требовалось доказать.
2) Диагонали ромба взаимно перпендикулярны. АС⊥BD.
FC⊥AC, так как FC перпендикулярна плоскости АВСD (дано).
Проведем В1D1 параллельно BD. Тогда АС⊥B1D1, а AF⊥B1D1 по теореме о трех перпендикулярах, так как АС - проекция наклонной AF на плоскость АВСD, а АС⊥B1D1, а значит и BD.
Что и требовалось доказать.