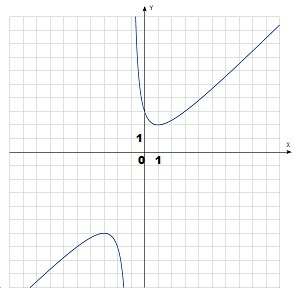
1) Область определения: x+1≠0 ⇒ x≠-1
D(f) = (-∞; -1)∪(-1;+∞)
2) Область значений (см. п. 6):
E(f) = (-∞; -6]∪[2; +∞)
3) Нули функции

x²=-3 ⇒ пересечений с осью ОХ нет.
4) Пересечение с осью OY
x=0

Функция пересекает ось OY в точке (0; 3)
5) y>0;

при x+1>0;
x∈(-1; ∞)
y<0; <img src="
https://tex.z-dn.net/?f=%5Cfrac%7Bx%5E2%2B3%7D%7Bx%2B1%7D%5C+%5Ctextless+%5C+0" id="TexFormula5" title="\frac{x^2+3}{x+1}\ \textless \ 0" alt="\frac{x^2+3}{x+1}\ \textless \ 0" align="absmiddle" class="latex-formula"> при x+1<0;<br> x∈(-∞; -1)
6) Экстремумы

(x+1)²-4=0; (x+1)² = 4; x+1 = 2 или x+1 = -2
x₁ = 1;

x₂ = -3;

В точке x₁ = 1: y' меняет знак с минуса на плюс ⇒
(1; 2) - точка минимума
В точке x₂ = -3: y' меняет знак с плюса на минус ⇒
(-3; -6) - точка максимума
7) Функция убывает при x∈[-3; -1)∪(-1; 1]
Функция возрастает при x∈(-∞;-3]∪[1;+∞)
8) Функция не является периодической

Функция не является четной.
Функция не является нечетной
9) вертикальная асимптота в точке разрыва x=-1
Левосторонний и правосторонний пределы бесконечны

Наклонная асимптота y = kx + b


Уравнение наклонной асимптоты
y=x-1
10)

y''>0;

при x>-1
⇒ график функции вогнутый при x∈(-1; +∞)
y''<0; <img src="
https://tex.z-dn.net/?f=%5Cfrac%7B8%7D%7B%28x%2B1%29%5E3%7D+%5C+%5Ctextless+%5C+0" id="TexFormula15" title="\frac{8}{(x+1)^3} \ \textless \ 0" alt="\frac{8}{(x+1)^3} \ \textless \ 0" align="absmiddle" class="latex-formula"> при x<-1<br>⇒ график функции выпуклый при x∈(-∞; -1)