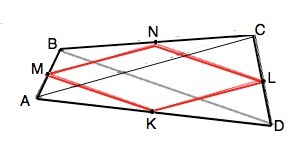
Если в произвольном четырёхугольнике соединить поочередно середины сторон отрезками, то эти отрезки будут средними линиями треугольников, на которые делят четырехугольник диагонали, а противоположные стороны образовавшегося четырёхугольника будут равны и параллельны. Такой вписанный четырехугольник будет параллелограммом.
В данном случае МN=AC:2, NL= BD:2, LK=AC:2, KM=BD:2. Ромб – параллелограмм с равными сторонами.
Следовательно, четырёхугольник МNLK будет ромбом, если диагонали исходного четырёхугольника равны.