Два равносторонних треугольника со сторонами 10 и 8 пересекаются, образуя шестиконечную...

Question

Два равносторонних треугольника со сторонами 10 и 8 пересекаются, образуя
шестиконечную звезду, при этом острые углы при пересечении любых двух сторон этих
треугольников оказались равны углам исходных треугольников. Найдите периметр
шестиугольника, образованного пересечением этих двух треугольников.

Answer 1

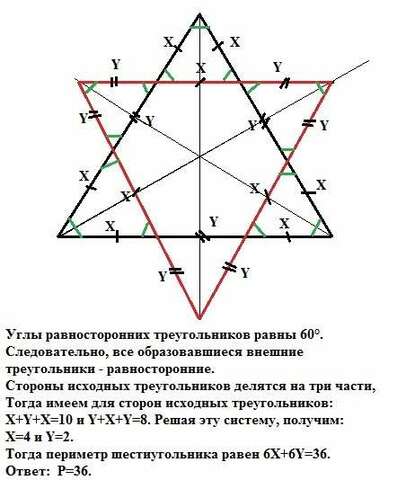
Внутренние углы равносторонних треугольников равны по 60°.
Следовательно, все образовавшиеся внешние треугольники - равносторонние, так как дано, что острые углы при пересечении любых двух сторон этих треугольников оказались равны углам исходных треугольников, то есть 60°.
Стороны исходных треугольников делятся на три части,
Тогда имеем для сторон исходных треугольников:
X+Y+X=10 и Y+X+Y=8. Решая эту систему, получим:
X=4 и Y=2.
Тогда периметр шестиугольника равен 6X+6Y=36.
Ответ:  Р=36.

---