Через конечную точку C диагонали AC=15,7 ед. изм. квадрата ABCD проведена прямая...

Question

Через конечную точку C диагонали AC=15,7 ед. изм. квадрата ABCD проведена прямая перпендикулярно диагонали AC. Проведённая прямая пересекает прямые AB и AD в точках M и N соответственно. Определи длину отрезка MN.

Answer 1

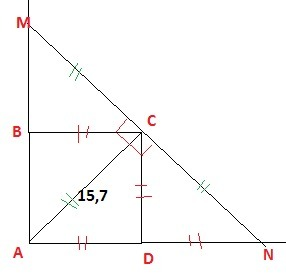
∠ACD=∠CAD=45°, так как  диагональ квадрата делит угол пополам.
В ΔACN  ∠CAD=45°, ∠ACN=90°, так как  AC⊥MN по условию,⇒  
ΔDNC=45°, значит ΔАCN - равнобедренный и  CN=AC=15,7ед. изм.
В ΔACM  ∠A=45°, ∠ACM=90°⇒∠AMC=45°, значит ΔАСМ-равнобедренный, MC=AC=15,7ед. изм. 
MN=MC+CN=15,7+15,7=31,4 ед. изм.

---