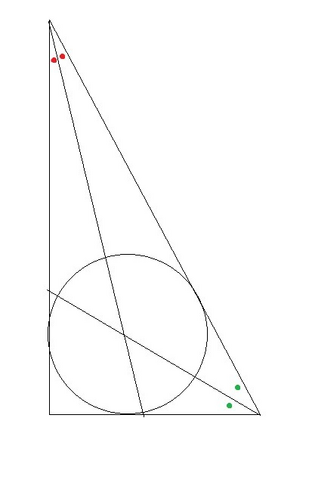
Центр вписанной окружности - точка пересечения биссектрис. На рисунке указаны биссектрисы, выходящие из острых углов прямоугольного треугольника. Пусть угол отмеченный зеленым α, а красным β; 2α+2β = 90°; Значит α+β=45°; Значит тупой угол треугольника, образованного биссектрисами равен 180°-45°=135°. Стороны, прилежащие к этому углу, по условию равны √54 и √10. По теореме косинусов имеем: гипотенуза =

Далее слишком большие вычисления. Они аналогичны тем, что выше. Тоже через теорему косинусов, ну можно местами и синусов :)