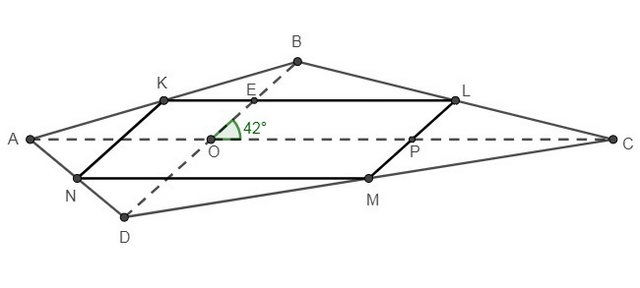
Пусть дан четырехугольник ABCD,
BD = 2 cм
АС = 5 см
∠ВОС = 42°
Точки К, L, M и N - середины сторон АВ, ВС, CD и AD соответственно.
Найти: стороны и углы четырехугольника KLMN
Средняя линия треугольника соединяет середины двух его сторон и параллельна третьей.
KN - средняя линия ΔDAB, LM - средняя линия ΔBCD, тогда:
KN = LM = BD/2 = 2/2 = 1cм
Аналогично:
KL - средняя линия ΔABC, MN - средняя линия ΔACD, тогда:
KL = MN = AC/2 = 5/2 = 2.5 cм
KLMN - параллелограмм
Рассмотрим четырехугольник OELP:
OE || LP и OP || EL ⇒ OELP - параллелограмм
Противоположные углы параллелограмма равны, тогда:
∠KLM = ∠ВОС = 42°
В параллелограмме KLMN:
∠KNM = ∠KLM = 42° (противоположные углы равны)
∠NKL= ∠NML = 180 - 42 = 138° (сумма соседних углов = 180°)
Ответ: KN = LM = 1 см; KL = MN = 5 см; ∠KNM = ∠KLM = 42°; ∠NKL= ∠NML = 138°