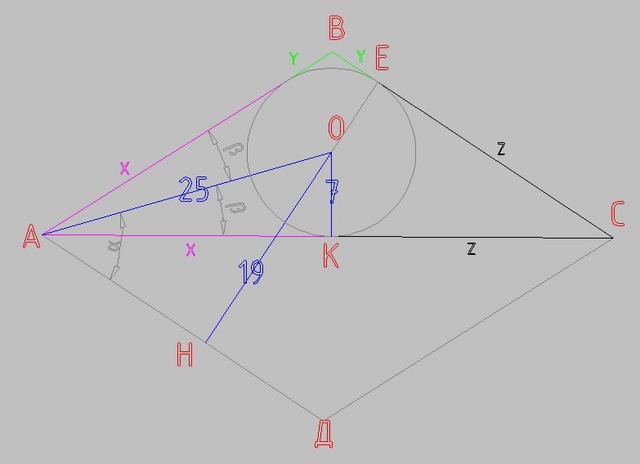
--- 1 ---
из ΔАОК
x² + 7² = 25²
x² = 625 - 49 = 576
x = 24
--- 2 ---
подготовительная работа
sin(α) = 19/25
cos(α) = √(1-19²/25²) = √(625 - 361)/25 = √264/25 = 2√66/25
--- 3 ---
и ещё синусы
sin(β) = 7/25
cos(β) = 24/25
cos(2β) = cos²(β) - sin²(β) = (24/25)² - (7/25)² = 527/625
--- 4 ---
Надо больше синусов!!!
sin(α + β) = sin (α) · cos (β) + cos (α) · sin (β)
sin(α + β) = 19/25 · 24/25 + 2√66/25 · 7/25 = (456+14√66)/625
--- 5 ---
ЕН - высота параллелограмма
АВ*sin(α+β) = ОН + ОЕ
(x+y)*sin(α+β) = 19 + 7
(24+y)*(456+14√66)/625 = 26
24+y = 26*625/(456+14√66)
Иррациональность в знаменателе... нехорошо. Домножим на сопряжённое
24+y = 26*625*(456-14√66)/(456² - (14√66)²)
24+y = 26*625*(456-14√66)/(207936 - 196*66)
24+y = 26*625*(456-14√66)/(207936 - 12936)
24+y = 26*625*(456-14√66)/195000 = 26*(456-14√66)/312 = (456-14√66)/12
24+y = 38 - 7√66/6
y = 14 - 7√(11/6)
И это прекрасно :)
--- 6 ---
Теорема косинусов, треугольника АВС, сторона ВС
ВС² = AC² + AB² - 2*AB*AC*cos(∠BAC)
(y+z)² = (x+y)² + (x+z)² - 2(x+y)*(x+z)*cos(2*β)
(y+z)² = (24+y)² + (24+z)² - 2(24+y)*(24+z)*527/625
y² + 2yz + z² = 576 + 48y + y² + 576 + 48z + z² - 2*527/625*(576 + 24y + 24z + yz)
2yz = 576 + 48y + 576 + 48z - 2*527/625*(576 + 24y + 24z + yz)
yz = 576 + 24y + 24z - 527/625*(576 + 24y + 24z + yz)
625yz = 625*576 + 625*24y + 625*24z - 527*(576 + 24y + 24z + yz)
625yz = 360000 + 15000y + 15000z - 303552 - 12648y - 12648z - 527yz
1152yz = 2352y + 2352z + 56448
24yz = 49y + 49z + 1176
y(24z - 49) = 49z + 1176
Подставляем y
(14 - 7√(11/6))(24z - 49) = 49z + 1176
(2 - √(11/6))(24z - 49) = 7z + 168
48z - 98 - 4√66z + 49√(11/6) = 7z + 168
41z - 4√66*z = 266 - 49√(11/6)
z = (266 - 49√(11/6)) / (41 - 4√66)
Домножаем на сопряжённый множитель
z = (266 - 49√(11/6))(41 + 4√66) / (41² - (4√66)²)
z = (266*41 + 266*4√66 - 49*41√(11/6) - 49*4*11) / (1681 - 16*66)
z = (10906 + 1064√66 - 2009√(11/6) - 2156) / 625
z = (10906 + 1064*6√(11/6) - 2009√(11/6) - 2156) / 625
z = (8750 + 4375√(11/6)) / 625
z = 14 + 7√(11/6)
--- 7 ---
Стороны параллелограмма
АВ = x + y = 24 + 14 - 7√(11/6) = 38 - 7√(11/6)
АД = ВС = y + z = 14 - 7√(11/6) + 14 + 7√(11/6) = 28
Площадь
S = АВ*АД*sin(∠ВАД)
S = (38 - 7√(11/6))*28*(456+14√66)/625
S = 28/625*(38*456 - 7*14*11 - 7*456√(11/6) + 38*14√66)
S = 28/625*(17328 - 1078 - 532√66 + 532√66)
S = 28*26
S = 728