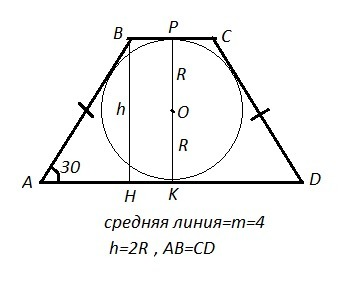
ABCD - трапеция, AB=CD ,
ABCD описана около окружности с центром в точке О ⇒ сумма боковых сторон равна сумме оснований: AB+CD=BC+AD.
Средняя линия трапеции m=(BC+AD):2=4 см ⇒ BC+AD=8 см.
АВ+CD=8 cм
Так как АВ=СD , то АВ=CD=8:2=4 cм.
Опустим перпендикуляр ВН на основание AD.
Рассм. ΔАВН. ∠АНВ=90°, ∠ВАН=30° (по условию).
ВН - катет, лежащий против угла в 30° ⇒ он равен половине гипотенузы: ВН=0,5·АВ=0,5·4=2 см.
Но катет ВН является высотой h трапеции. А высота трапеции, описанной
около окружности равна диаметру этой окружности:
ВН=2R=2 cм ⇒ R=2:2=1 cм .
Длина окружности с радиусом R=1 cм равна l=2ПR=2П·1=2П