Найдите площадь треугольнике в ABD и CBD и четырёхугольника ABCD, если известны...

Смотрите фото:

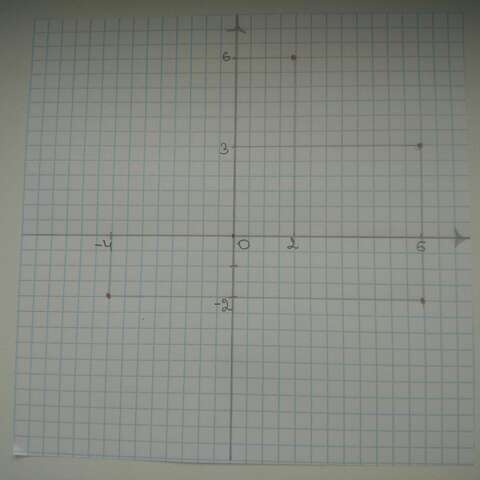
1. Рисуем точки по указанным координатам.

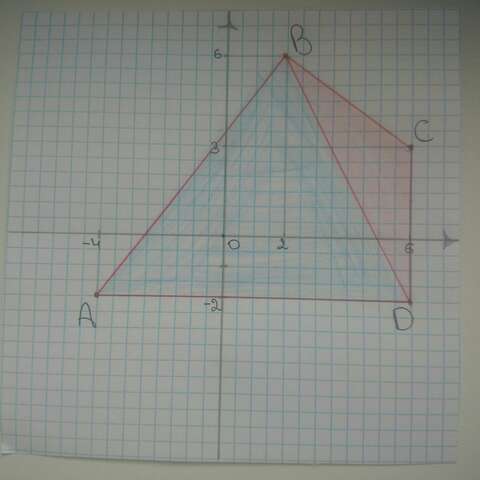
2. Соединяем точки и получаем четырехугольник (и два рассматираемых треугольника).

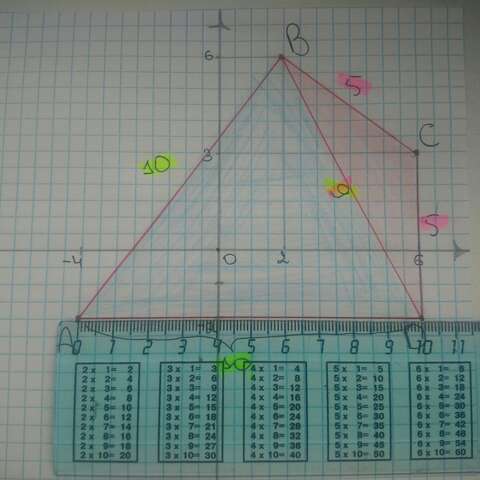
3. Измеряем полученные стороны и диагональ фигуры ⇒ получаем "дано".

ΔABD и ΔCBD - равнобедренные по определению, тогда их площадь находится следующим образом:

$S=\frac{b\sqrt{a^{2}-\frac{b^{2}}{4}}}{2}$ ,

где а - боковые стороны треугольников;

b - их основания.

Начнем с синего Δ (ΔABD):

$S_{1}=\frac{9\sqrt{10^{2}-\frac{9^{2}}{4}}}{2}=\frac{9\sqrt{100-20,25}}{2}=\frac{9*8,93}{2}=\frac{80,37}{2}=40,185$ (см²)

Затем красный Δ (ΔCBD):

$S_{2}=\frac{9\sqrt{5^{2}-\frac{9^{2}}{4}}}{2}=\frac{9\sqrt{25-20,25}}{2}=\frac{9*2,17}{2}=\frac{19,53}{2}=9,77$ (см²)

Ответ: S1=40,185 см², S2=9,77 см²