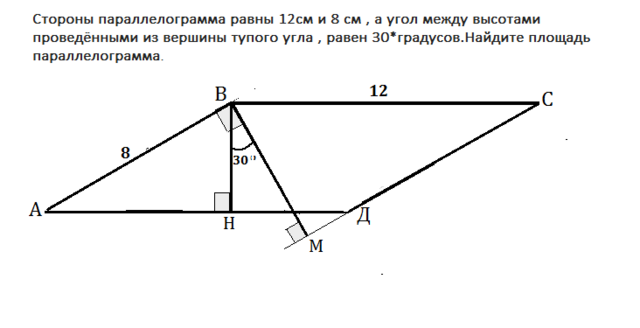
Пусть данный параллелограмм будет АВСД.
Сделаем соразмерно условию рисунок и рассмотрим его.
ВН высота, ⊥ АД и⊥ ВС,
ВМ - высота и ⊥АВ и ⊥ прямой СД. ⇒
Угол АВМ - прямой, угол АВН=90-60º, ⇒
угол ВАН=30º
ВН противолежит углу 30º, на этом основании рана половине АВ=4 см
Площадь параллелограмма равна произведению его высоты на сторону, к которой она проведена.
S АВСД=4*12=48 см²
Так как противоположные углы параллелограмма равны, точно так же высота к ВД ( она пересекает продолжение СД) равна 12:2=6 см,
Ясно, что произведение высоты ВМ и стороны СД = 6*8=48 см²