Формула площади параллелограмма:  , так как прямоугольник - частный случай параллелограмма и его диагонали равны, то формула перепишется так:
, так как прямоугольник - частный случай параллелограмма и его диагонали равны, то формула перепишется так: 
Из площади найдём диагональ прямоугольника:  (см).
(см).
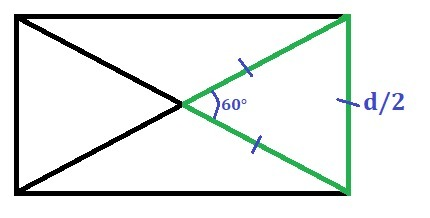
Рассмотрим треугольник, образованный двумя половинками диагоналей и одной из сторон треугольника (выделен зелёным на рисунке). Так как мы имеем дело с прямоугольником, половинки диагоналей равны, значит треугольник равнобедренный. Так как угол между диагоналями равен 60°, то данный треугольник - равносторонний, ведь все углы равностороннего треугольника по 60°.
Значит ширина прямоугольника равна половине диагонали, то есть:  (см).
(см).
Длину найдём по теореме Пифагора из треугольника образованного диагональю и двумя смежными сторонами прямоугольника:  (см).
(см).
Так же длину можно было найти из площади:  (см).
(см).
Ответ: длина 7√3 см, ширина 7 см.