Биссектриса одного из углов делит параллелограмм на две части, разность периметров...

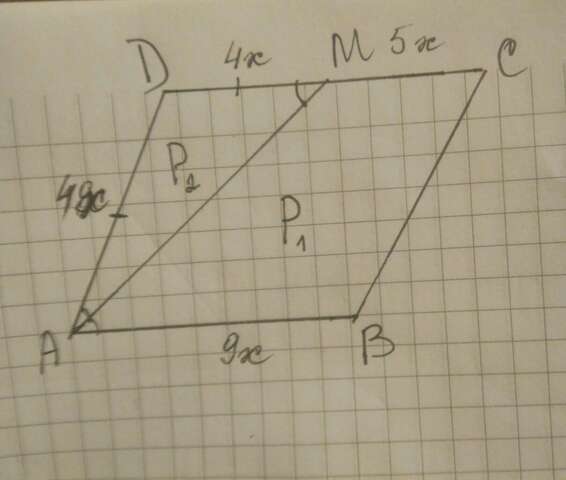
Дано: параллелограмм АВСD (DC=AB; AD=BC)
биссектриса АМ
Р1-Р2=10 см

Найти: Р(abcd)

Решение:
Пусть DC=9x; CB=4x, тогда

$P_{abcd}$
= 2(4x + 9x) = 8x + 18x = 26x

ABCD - параллелограмм;
АM - биссектриса угла DAB
=>треугольник AMD равнобедренный по свойству параллелограмма.
AD=DM=4х

МС=DC-DM=9x-4x=5x

Пусть АМ - у, тогда P1 - P2 = (5х+4х+9х+у) - (4х+4х+у)=10
18х+у-8х-у=10
10х=10
х=10/10=1

Р(abcd)=26x=26×1=26 см

Биссектриса одного из углов делит параллелограмм ** две части, разность периметров...