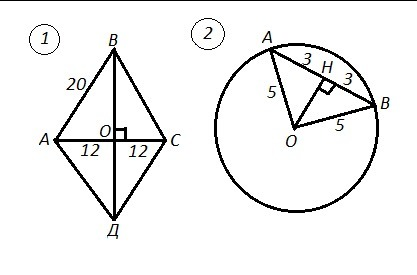
1) АВСД - ромб, сторона которого АВ=20 см, диагональ АС=24 см.
В ромбе диагонали перпендикулярны и в точке пересечения делятся пополам. Поэтому , если диагональ АС=24 см, то АО=ОС=12 см, и ∠АОВ=90°.
Из ΔАОВ по теореме Пифагора : ВО=√(АВ²-АО²)=√(20²-12²)=16.
Диагональ ВД=2·ВО=2·16=32 (см).
2) Хорда АВ=6 см. Радиус АО=ВО=5 см.
ОН⊥АВ. Перпендикуляр к хорде делит эту хорду пополам (теорема) ⇒ АН=ВН=6:2=3 (см).
ΔАОН: ∠АНО=90° ⇒ ОН=√(АО²-АН²)=√(5²-3²)=4 (см) .