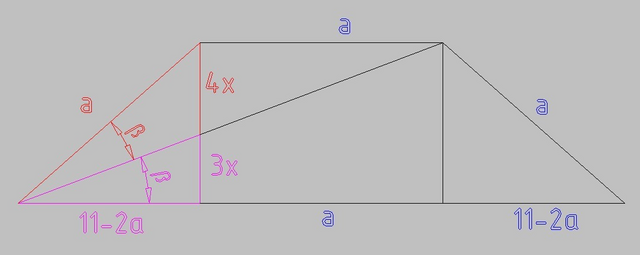
Боковая сторона равна малому основанию, т.к. накрест лежащие углы при основаниях равны.
Периметр равен 22, малая сторона а, проекция боковой стороны на основание (22 - 4a)/2 = 11 - 2a
рассмотрим два прямоугольных треугольника, образованных высотой, проекцией боковой стороны на основание и для малинового - диагональю, для красного - боковой стороной.
Для малого
tg (β) = 3x/(11-2a)
Для большого
tg (2β) = 7x/(11-2a)
Разделим одно уравнение на другое
tg (2β)/tg (β) = (7x/(11-2a)) / (3x/(11-2a))
tg (2β)/tg (β) = 7/3
---
по формуле тангенса половинного угла
tg (2β) = 2*tg (β) / (1 - tg² (β))
---
2*tg (β) / (1 - tg² (β)) /tg (β) = 7/3
1 - tg² (β) = 6/7
tg² (β) = 1/7
tg (β) = 1/√7
tg (2β) = 2*tg (β) / (1 - tg² (β)) = 2/√7 / (1 - (1/√7)²) = 2/√7 * 7/6 = √7/3
---
выразим косинус двойного угла через тангенс β
cos (2β) = (1 - tg² (β)) / (1 + tg² (β)) = (1 - 1/7) / (1 + 1/7) = 6/7 / 8/7 = 3/4
Косинус двойного угла - это отношение проекции боковой стороны к боковой стороне
cos (2β) = (11-2a)/a = 3/4
44 - 8a = 3a
44 = 11a
a = 4
Это малое основание
Большое основание
b = 22 - 3*a = 22 - 12 = 10
Средняя линия
c = 1/2(a+b) = 1/2(4+10) = 7