Помогите с геометрии, даю 50 баллов. Дали на каникулы.8 класс. Тема: Решение...

Помогите с геометрии, даю 50 баллов. Дали на каникулы.8 класс. Тема: Решение прямоугольных треугольников1) На рисунке (на фото) - прямоугольный треугольник ABC (∠C = 90 °). найдите:1. cos A2. sin B3. tg A4. cos B2) Точка находится на расстоянии 4 см от прямой. С этой точки до прямой проведения наклонную, что образует с прямой угол 45 °. Найдите длину наклонной и длину проекции наклонной на прямую.3) В прямоугольном треугольнике ABC (∠C = 90 °) AC = 8 см, cos∠A = 4/5. Найдите второй катет и гипотенузу треугольника

$cosA=\frac{AC}{AB}=\frac{15}{17}\; ;\; sinB=\frac{AC}{AB}=\frac{15}{17}\; ;\; tgA=\frac{BC}{AC}=\frac{8}{15}\; ;\; cosB=\frac{BC}{AB}=\frac{8}{17}$

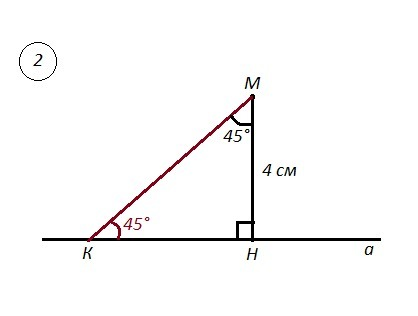
2) Точка М , прямая а , МН⊥ а , МН=4 см , МК - наклонная, ∠МКН=45°.

Так как ∠МКН=45°, то и ∠КМН=90°-∠МКН=45° .

Тогда ΔМКН - равнобедренный и МН=КН=4 см, то есть проекция наклонной - это КН=4 см.

Наклонная МК=√(МН²+КН²)=√(4²+4²)=√2·16=4√2 (см).

Или МК=МН:sin∠МКН=4:(√2/2)=(4·2)/√2=4√2 (см) .

3) ΔАВС , ∠С=90° , АС=8 см , cos∠А=4/5 .

$cosA=\frac{AC}{AB}=\frac{8}{AB}\; \; \to \; \; AB=\frac{8}{cosA}=\frac{8}{4/5}=\frac{8\cdot 5}{4}=10\\\\BC=\sqrt{AB^2-AC^2}=\sqrt{10^2-8^2}=\sqrt{100-64}=\sqrt{36}=6$

Помогите с геометрии, даю 50 баллов. Дали ** каникулы.8 класс. Тема: Решение...