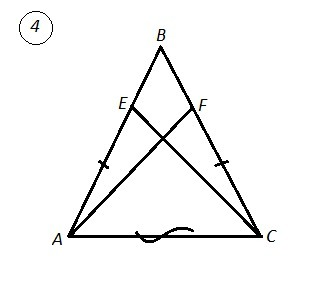
4. ΔАВС , АВ=ВС , АЕ=СF .
∠ВАС=∠АСВ так как Δ равнобедренный.
Рассм. ΔAFC и ΔАЕС. Они равны по 1 признаку равенства треу-ов: АЕ=CF (по условию) , АС - общая сторона , ∠EAC=∠ACF .
Значит будут равны и соответствующие углы (против равных сторон лежат равные углы): ∠АСЕ=∠CAF.
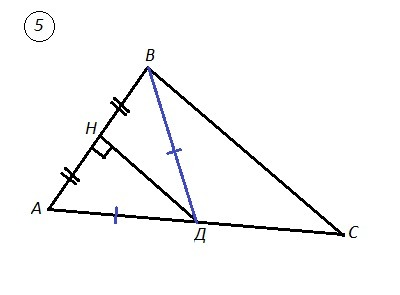
5. ΔАВС , ДН⊥АВ , АН=ВН , АС=8 , ВС=6 .
Соединим точки В и Д , получим ΔАВД. Он будет равнобедренным, т.к. ДН - одновременно высота и медиана этого треугольника ⇒ АД=ВД .
Периметр ΔВДС равен:
Р=ВД+ДС+ВС=АД+ДС+ВС=(АД+ДС)+ВС=АС+ВС=8+6=14 см .