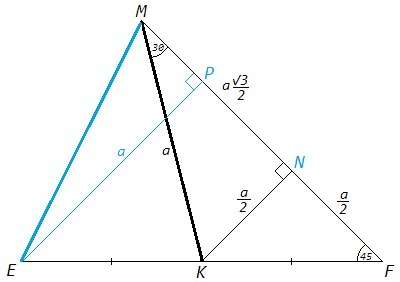
MK=a, KN⊥MF, EP⊥MF
KN=a/2, MN=a√3/2 (△MKN c углами 30,90)
NF=KN=a/2 (△KNF c углами 45,90)
KN - средняя линия в △EPF, EP=2KN=a
PF=EP=a, EF=a√2 =13/2 (△EPF c углами 45,90)
MP=MF-PF =MN+NF-PF =a√3/2 +a/2 -a =a(√3-1)/2
EM=√(MP^2+EP^2) =√(a^2(√3-1)^2/4 +a^2) =a√(2 -√3/2)
EM= 13√2/4 *√(2 -√3/2) =13/4 *√(4-√3)
Или
По теореме синусов
KF/sin(KMF) = MK/sin(MFK) <=>
2KF = 13√2*2/4*√2 <=> KF=13/4
EK=13/4, EF=2KF =13/2
cos(EKM) =cos(30+45) =cos30*cos45-sin30*sin45 =√2/4 *(√3-1)
По теореме косинусов
EM^2= EK^2 +MK^2 -2EK*MK*cos(EKM) <=>
EM^2= (13/4)^2 *(1+2-(√3-1)) <=>
EM= 13/4 *√(4-√3)