В равнобедренном треугольнике KLM (KL=KM) точка N — середина стороны KL. Прямая,...

Question

В равнобедренном треугольнике KLM (KL=KM) точка N — середина стороны KL. Прямая, касающаяся описанной около треугольника окружности в точке L, пересекает прямую KM в точке P. PK=8. Найдите проекцию PN на KL.

Answer 1

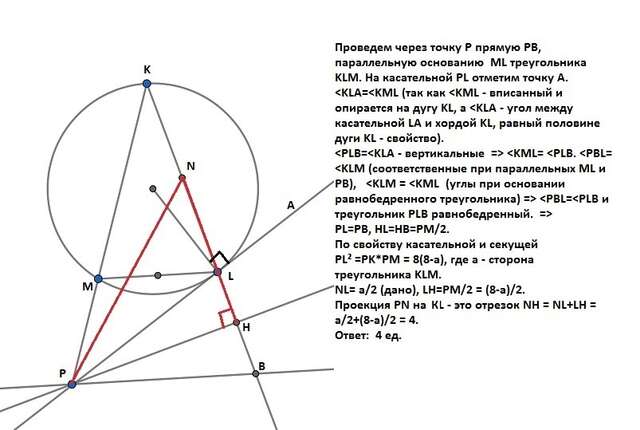
Проведем через точку Р прямую PB, параллельную основанию  MLтреугольника KLM. На касательной PL отметим точку А.

  PL=PB,   HL=HB=PM/2.

По свойству касательной и секущей PL² =PK*PM = 8(8-a), где а - сторона треугольника KLM.  

NL= a/2 (дано), LH=PM/2 = (8-a)/2.  Проекция PN на КL - это отрезок NH = NL+LH = a/2+(8-a)/2 = 4.

Ответ:  4 ед.

---