1) В равнобедренный треугольник, основание которого равно 12 см, а боковая сторона – 18...

Question

1) В равнобедренный треугольник, основание которого равно 12 см, а боковая сторона – 18 см, вписана окружность. Найдите расстояние между точками касания этой окружности к боковым сторонам треугольника. 2) Через точку A, которая лежит вне окружности, проведены две прямые, одна из которых касается окружности в точке B, а вторая пересекает окружность в точках C и D (точка C лежит между точками A и D), AB-18 см, AC:CD=4:5. Найдите отрезок AD.

Comments

К каждому заданию рисунок

Answer 1

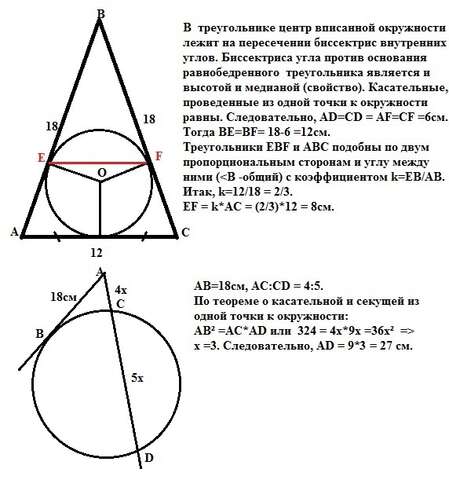
1. В  треугольнике центр вписанной окружности лежит на пересечении биссектрис внутренних углов. Биссектриса угла против основания равнобедренного  треугольника является и высотой и медианой (свойство). Касательные, проведенные из одной точки к окружности равны. Следовательно, AD=СD = AF=CF =6см.

Тогда ВЕ=BF= 18-6 =12см.

Треугольники EBF и АВС подобны по двум пропорциональным сторонам и углу между ними (<В -общий) с коэффициентом k=EB/AB. </p>

Итак, k=12/18 = 2/3.

EF = k*AC = (2/3)*12 = 8см.

2. По теореме о касательной и секущей их одной точки имеем:

АВ² = AC*AD. Из условия задачи АС=4х, СD=5х => AD= 9x.

Тогда 324 = 4х*9х = 36х²  =>  x = 3см.

Ответ: AD = 9*3 =  27см.

---