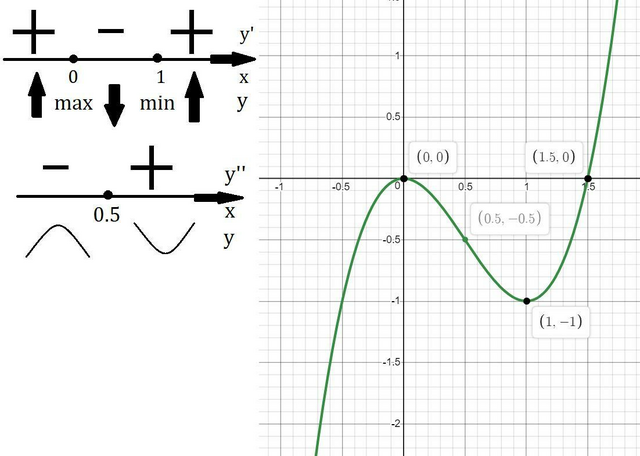
Соответственно корни уравнения 0 и 1,5.

Нашли экстремумы функции, включая их координаты. Определение min и max смотри внизу.

Нашли точку перегибая, до она выпуклая, а после вогнутая.
Функция растёт примерно как x^3, чтобы понимать как быстро возрастает график.
Точки пересечения с осью Ох мы нашли, найдём точки пересечения с осью Оу: 
У нас есть всё, чтобы построить график.