Ответ: 50°
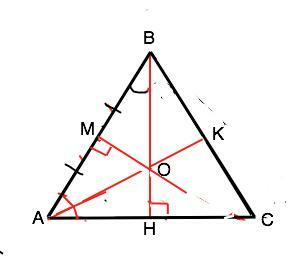
Объяснение: Пусть все три данных отрезка пересекаются в точке О. Обозначим ВН высоту из В, АК - биссектрису, МО - срединный перпендикуляр к АВ.
Треугольник АОВ - равнобедренный, т.к. его высота ОМ - медиана ( проходит через середину АВ), поэтому∠ВАО=∠АВО. Примем их равными α каждый. Так как АК - биссектриса, ∠ОАН=∠ВАО=α, а угол ∠ВАН=2 α. В прямоугольном треугольнике сумма острых углов равна 90°. 3α=90°, ⇒ α=30°
В прямоугольном ∆ СВН ∠СВН=90°-∠ВСН=90°-70°=20°
Угол АВС=∠АВН+∠СВН=30°+20°=50°