Чему равен угол между биссектрисой и высотой?
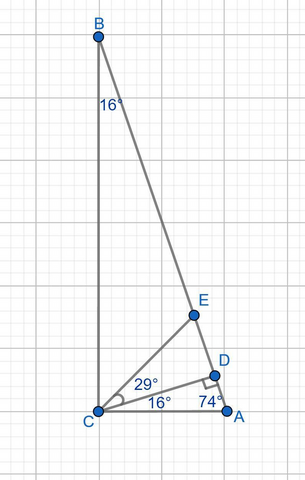
Вот похожая задача: Из вершины наибольшего угла прямоугольного треугольника проведены биссектриса и высота угол между которыми равен 29 градусов Найдите острые углы треугольника.
Решение:
В прямоугольном треугольнике наибольший угол = 90°. В ΔABC ∠С = 90°, CE - биссектриса, CD - высота. ∠ECD = 29°.
В ΔDCA ∠CDA = 90° (CD - высота), ∠DCA = 45° - 29° = 16°, ⇒∠A = 180° - 90° - 16° = 74°.
В ΔABC ∠B = 180° - 90° - 74° = 16°.
Ответ: ∠B = 16°, ∠A = 74°.