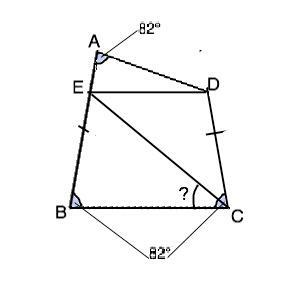
По условию три угла четырехугольника ABCD равны по 82°. Из суммы углов четырехугольника четвёртый угол D=360°-3•82°=114°
Из вершины D проведем DE параллельно ВС. Т.к. углы В и С равны по условию, а DE║ВС по построению, четырехугольник ВЕDC- равнобедренная трапеция и ВЕ=СD, что соответствует условию.
В ∆ АЕD ∠АЕD=∠В=82° как соответственные углы при пересечении параллельных ВС и ЕD секущей ВE.
В треугольнике АЕD. углы при АЕ равны, ⇒ он равнобедренный, ⇒ . Угол АDE=180°-2•82°=16°. Отсюда следует ED=АD=DC
По равенству боковых сторон ∆ ЕDC равнобедренный,⇒ углы при его основании ЕС равны.
В равнобедренном ∆ ЕDC угол ЕDC =114°-16°=98°, а ∠DCE=DEC=98°:2=49° Искомый ∠ВСЕ=∠BCD-∠DCE=82°-49°=33°