Найти область определения функции

Здесь надо учесть четыре ограничения:

1) Подкоренное выражение не должно быть отрицательным:

$x^2-4^2\geqslant 0\\(x-4)(x+4) \geqslant 0\\x \in (- \infty; -4] \cup [4; + \infty)$

2) Выражение под логарифмом должно быть положительным: 0" alt="x>0" align="absmiddle" class="latex-formula">

3) Знаменатель первой дроби должен быть ненулевым

$\log_2 x+9\neq 0\\\log_2 x \neq -9\\x \neq 2^{-9}\\x \neq \dfrac{1}{512}$

4) Знаменатель второй дроби также должен быть ненулевым:

$x+ 2 \cdot 4 \neq 0\\x \neq -8$

Теперь объединим эти промежутки (лучше сделайте это на листке бумаги, чтобы видеть наглядно): по второму условию икс положителен, поэтому первое условие сокращается до $x \geqslant 4$

Третье условие не удовлетворяет предыдущему, поэтому вычёркивается.

Четвёртое условие также вычёркивается как отрицательное.

Ответ: $x \geqslant 4$

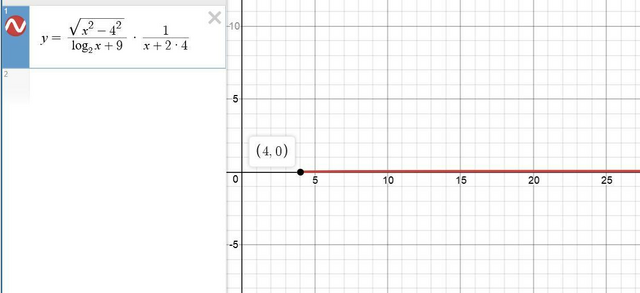
Вот так выглядит график этой функции, построенный на компьютере (см. скриншот).

P. S. Если появились какие-либо вопросы, задавайте.