Дана окружность w радиуса r=8. Прямая a, проходящая через точку A, лежащую вне окружности...

Question

Дана окружность w радиуса r=8. Прямая a, проходящая через точку A, лежащую вне окружности w, пересекает окружность w в точках B и C. Известно, что AB=4,AC=9 Чему равна длина отрезка касательной AK из точки A к окружности w? Чему равно расстояние от точки A до центра O окружности w? Помогите пожалуйста,30 баллов

Answer 1

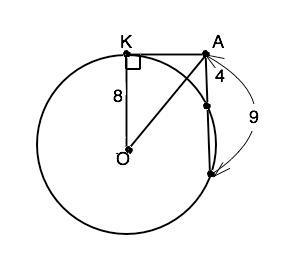
  Если из точки, лежащей вне окружности, проведены касательная и секущая, то квадрат длины касательной равен произведению секущей на ее внешнюю часть (по теореме о касательной и секущей: )

⇒ АК²=АС•АВ=9•4⇒ АК=√36=6

  Радиус, проведенный в точку касания, перпендикулярен касательной.

  Из ∆ АКО по т.Пифагора АО=√(AK²+KO²)=√(36+64)=10 (ед. длины)

---