Ответ:
Sabcd ≈ 736,6 см²
Объяснение:
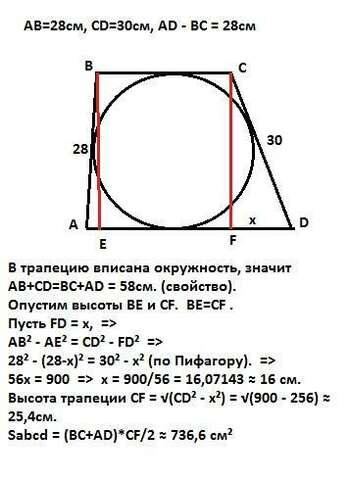
В трапецию вписана окружность, значит АВ+CD=BC+AD = 58см. (свойство).
Опустим высоты ВЕ и CF. BE=CF . Пусть FD = x, =>
AB² - AE² = CD² - FD² =>
28² - (28-x)² = 30² - x² (по Пифагору). =>
56x = 900 => x = 900/56 = 16,07143 ≈ 16 см.
Высота трапеции CF = √(CD² - x²) = √(900 - 256) ≈ 25,4cм.
Sabcd = (BC+AD)*CF/2 ≈ 736,6 см²