Відповідь:
60√3 см²
Пояснення:
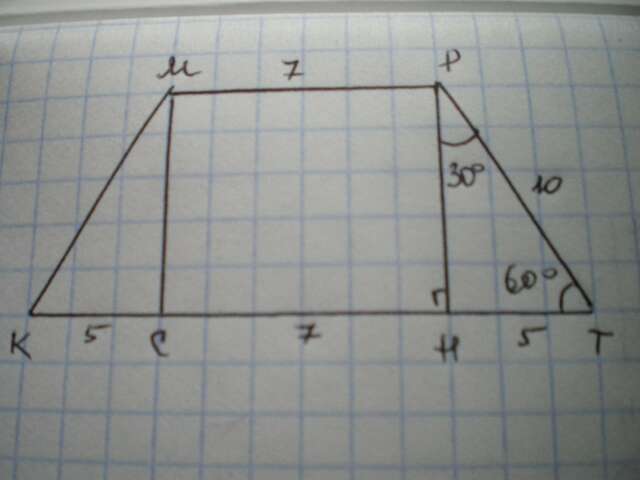
Дано: КМРТ - трапеція, КМ=РТ=10 см, МР=7 см. ∠Т=60°. Знайти S(КМРТ).
Проведем висоти МС=РН. ΔКМС=ΔРТН за катетом та гіпотенузою, отже КС=ТН.
∠ТРН=90-60=30°, отже ТН=1/2 РТ=10:2=5 см.
КС=ТН=5 см. КТ=КС+СН+ТН=5+7+5=17 см.
РН=√(РТ²-ТН²)=√(100-25)=√75=5√3 см.
S(КМРТ)=(МР+КТ):2*РН=(7+17):2*5√3=60√3 см²