Найди площадь круга, вписанного в равнобедренную трапецию с основаниями длиной 6 см и 12 см и периметром 36 см
Объяснение:
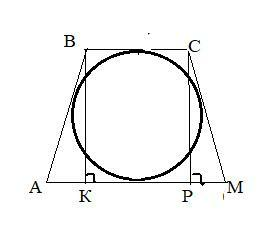
АВСМ- описанная трапеция⇒ суммы длин противоположных сторон равны. Т.е 6+12=АВ+СМ⇒ АВ=СМ=9 см. Пусть ВК⊥АМ , СР⊥АМ.
S(круга)=πr². Радиус вписанной в трапецию окружности будет равен половине высоты трапеции.
Т.к. ВК⊥АМ , СР⊥АМ, то КВСР-прямоугольник ⇒
КР=6 см, АК=РМ=(12-6) :2=3 (см).
ΔАВК-прямоугольный, по т. Пифагора ВК=√(9²-3²)=√18=3√2(см).
ВК-высота трапеции, значит r=(3√2)/2 см.
S(круга)= π ( (3√2)/2 )²=4,5π (см²)