Відповідь:
36√3 см²
Розв"язання:
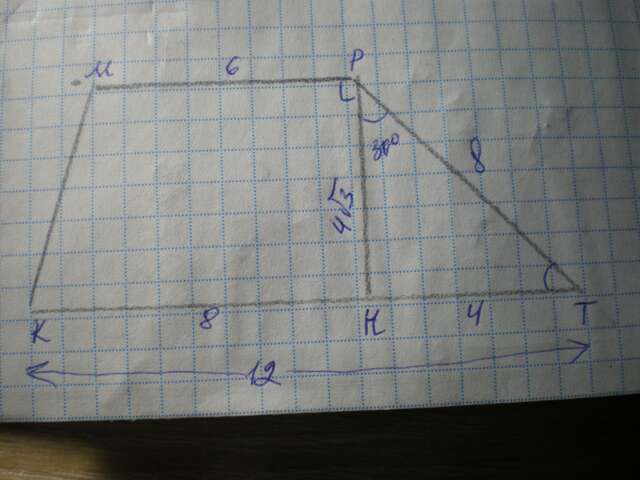
Дано: КМРТ - трапеція, МР=6 см, КТ=12 см, РТ=8 см, ∠МРТ=120°. Знайти S(КМРТ).
Проведемо висоту РН, розглянемо ΔРТН - прямокутний,
∠НРТ=120-90=30°, катет ТН, що лежить навпроти кута 30°, дорівнює половині гіпотенузи РТ. Отже, ТН=8:2=4 см.
Знайдемо РН за теоремою Піфагора:
РН=√(8²-4²)=√(64-16)=√48=4√3 см.
S=(МР+КТ)/2*РН=(6+12)/2*4√3=36√3 см²