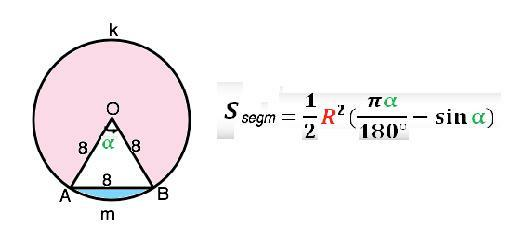Ответ: Длина дуг 8π/3 см и 40π/3 см S=16(2π-3√3)/3 см
Объяснение (подробно): Пусть АВ - хорда, проведенная в окружности с центром О. Соединив центр О с т.А и т.В, получим равнобедренный треугольник АОВ ( т.к. АО=ВО - радиусы). По условию АВ=8, АО=ОВ=8. ⇒ ∆ АОВ - равносторонний. Его углы равны по 60°.
Хорда АВ стягивает дугу 60° ⇒ Угол АОВ=60°.
Полная окружность равна 360°.⇒ Длина дуги АВ=60°:360°=1/6 длины окружности, а угол АОВ отсекает от неё сектор . площадью меньше площади окружности в 360°:60°= 6 раз.
С=2πR=2π•8=16πсм²
Длина дуги АmВ=С:6=16π/6=8π/3 см
Длина дуги АkВ=16π—8π/32=40π/3 см
Для нахождения площади сегмента существует формула (см. вложение). Но можно видеть, что площадь сегмента АmВ равна площади сектора АОВ без площади ∆ АОВ
Ѕ(окр)=π r²=π•8²=64π см².
Площадь сектора АОВ=Ѕ(окр):6=64π/6=32π/3 см²
Площадь ∆ АОВ=(АВ²•√3)/4=(64√3)/4=(32√3)/2 см²
S(сегм АmB)=16(2π-3√3)/3 см²