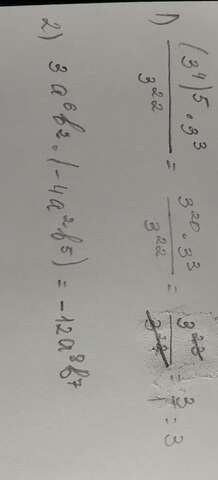Помогите, пожалуйста, решить задания 1 и 2, только с пояснениями, не просто одну цифру ,...

Ответ:

Подробное объяснение: в задании номер 1 число 3 в 4 степени возводится в 5 степень. Когда ты видишь что-то наподобие этого, то степени перемножаются: то есть 4 степень умножаем на 5 степень и получаем 20 степень, то есть 3 в 20 степени. Далее, в числителе, видим:

$3 {}^{20} \times 3 {}^{3}$

Здесь степени тоже умножаюся, потому что умножаются сами числа. Перемножаем и получаем 3 в 23 степени. Ну и затем остается сократить то, что получилось:

$\frac{3 {}^{23} }{3 {}^{22} }$

Сокращаем и получаем:

$\frac{3}{1} = 3$

Задание номер 2.

Ну, тут все просто, тут надо правильно перемножить, как на фото. С умножением степеней ситуация та же, что и в 1 задании.

Надеюсь, помогла:)