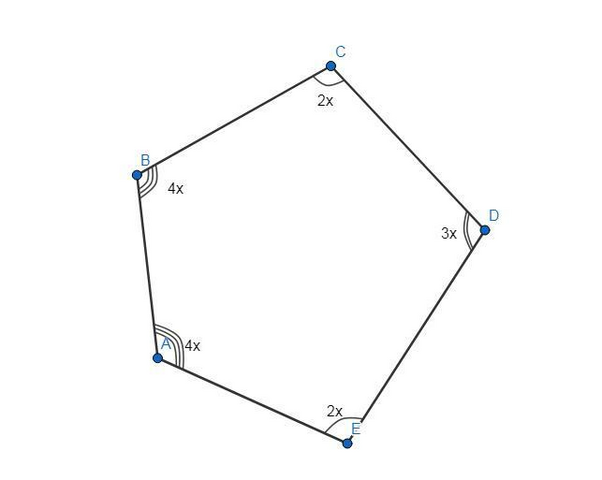
Дано:
ABCDE - выпуклый пятиугольник.
∠A : ∠В : ∠С : ∠D : ∠E = 4 : 4 : 2 : 3 : 2.
Найти:
∠A, ∠В, ∠С, ∠D, ∠E = ?
Решение:
Сумма углов выпуклого n-угольника вычисляется по формуле -

Где n - количество сторон.
Сумма углов выпуклого пятиугольника равна -

Если отношение углов ∠A : ∠В : ∠С : ∠D : ∠E = 4 : 4 : 2 : 3 : 2, то пусть каждый из них равен 4x, 4x, 2x ,3x, 2x соответственно.
4x+4x+2x+3x+2x = 540°
15x = 540°
x = 36°.
∠A = 4x = 4*36° = 144°
∠B = 4x = 4*36° = 144°
∠C = 2x = 2*36° = 72°
∠D = 3x = 3*36° = 108°
∠E = 2x = 2*36° = 72°.
Ответ: 144°, 144°, 72°, 108°, 72°.