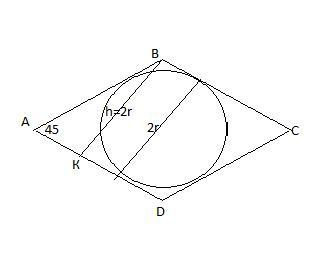
Основание прямой призмы — ромб с острым углом 45°, высота призмы равна 15 см.
Цилиндр с боковой поверхностью 90π см² вписан в призму. Определи площадь боковой поверхности призмы.
Объяснение:
S(бок.призмы)=Р(осн)*h , где h-высота призмы. Высота призмы совпадает с высотой цилиндра.
Найдем сторонууууу ромба.
В основании призмы-ромб с вписанной окружностью (касается сторон ромба ). Высота ромба составляет 2r .
S(бок.цилиндра)=2π * r* h , или
90π=2π * r* 15 или r=3 см. Тогда высота ромба 6см.
Рассмотрим ΔАВК-прямоугольний , sin45°=ВК/АВ ,√2/2=6/АВ , АВ=6√2 см. Тогда Р(ромба)=4*6√2=24√2 (см)
S(бок.призмы)=24√2*15=360√2 (см²)