Объяснение:
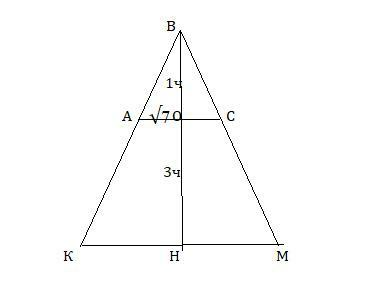
В осевом сечении получится равнобедренный ΔКВМ , с АС║КМ, ВН⊥КМ ,S(м)=7π, ВО/ОН=1/3.
S(круга)= π r², 7π=πr² , r=√7 , АО=√7.
ΔАВО подобен ΔКВН по двум углам: ∠А-общий,∠ВАО=∠ВКН как соответственные при АС║КМ, ВК-секущая.Значит сходственные стороны пропорциональны :
АО/КН=1/4=АО/КН
1/4=√7/КН
КН=4√7.
S(нижнего основания конуса)= π(4√7)²=112π .
2 способ.
Полученное сечение(круг) параллельно плоскости основания(кругу). Они подобны с к=1/4. Значит их площади относятся как к²⇒
S(м):S(б)=к² или 7π/S(б)=1/16 , S(б)=7π*16=112π.