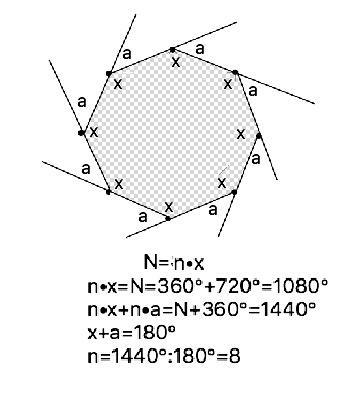
Ответ: 8 сторон
Объяснение: Сумма внешних углов выпуклого многоугольника ( любого) равна 360°.
Сумма внутренних углов данного многоугольника по условию
360°+720°=1080°.
Если N- сумма внутренних углов, то их количество находят по формуле
N=180°•(n-2), где n - число сторон многоугольника.
1080°=180°•n -360° , откуда
n=1448°:180°=8
Иногда удобнее применять другой способ ( с тем же результатом).
Сколько бы ни было сторон у выпуклого многоугольника, каждый внутренний угол с одним внешним при той же вершине составляет в сумме 180° ( развернутый угол).
Сумма внутренних (1080°) и внешних ( 360°) углов данного многоугольника = 1080°+360°= 1440°
Делим на величину развёрнутого угла:
1440°:180°=8 ( сторон),