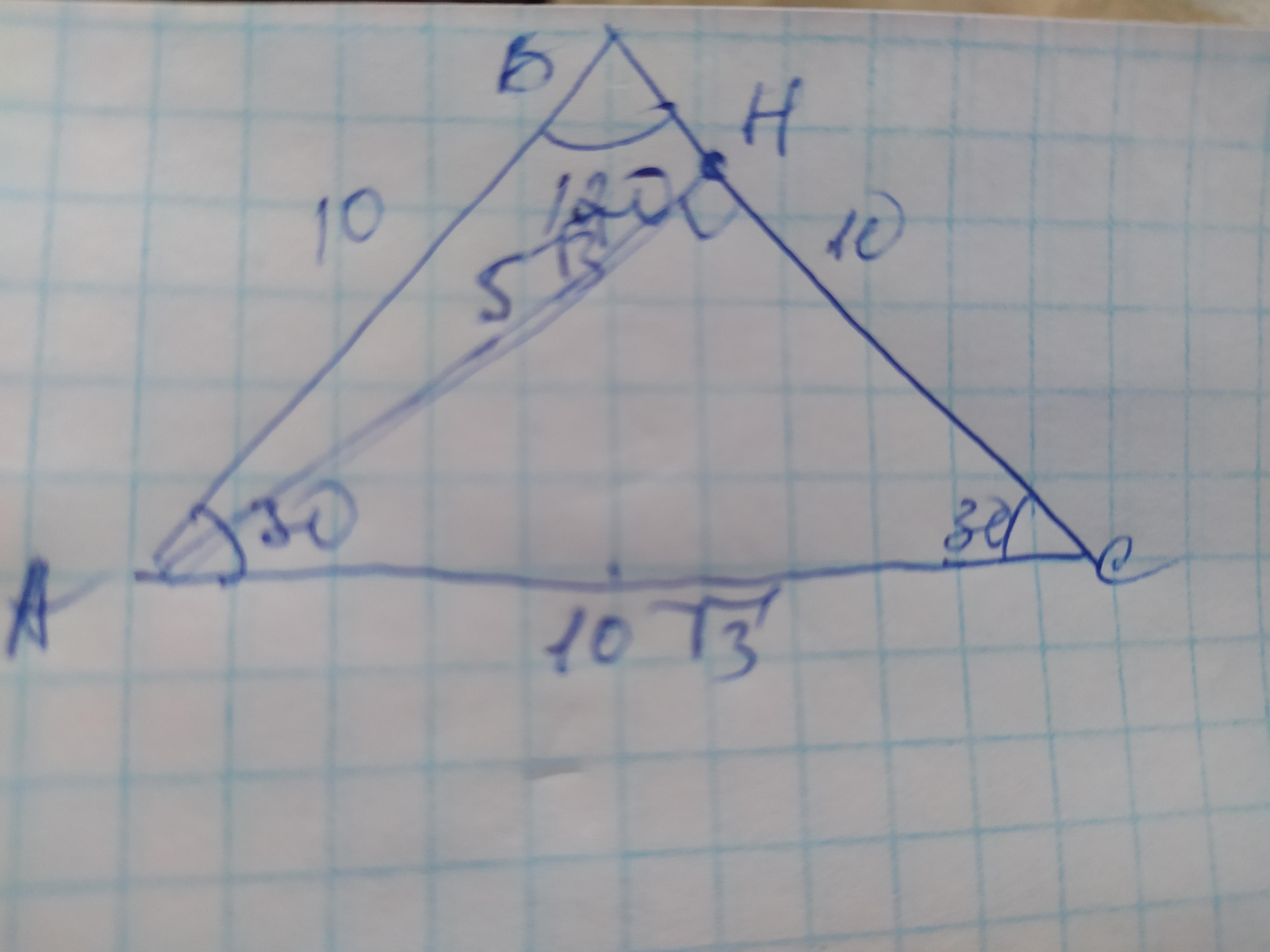
Ответ: 5√3см
Объяснение: Обозначим вершины треугольника А В С, угол в=120°, а высоту АН. Сумма углов треугольника составляет 180°, поэтому можно найти угол С.
Угол С=180-120-3=30°. ∆АВС равнобедренный поскольку угол А= углу С, поэтому АВ=ВС=10см. Используя теорему косинусов найдём АС. АС²=АВ²+ВС²–2×АВ×ВС×cosB=
=10²+10²-2×10×10×cos120°=
=100+100-2×100×(-½)=200+100=300
AC=√300=√3×√100=10√3см
∆АСН. Он прямоугольный, где АН и СН катеты, а АС - гипотенуза. В прямоугольном треугольнике катет лежащий напротив угла 30° равен половине гипотенузы. Этим катетом является высота АН, поэтому АН=10√3÷2=5√3см