Рассмотрим
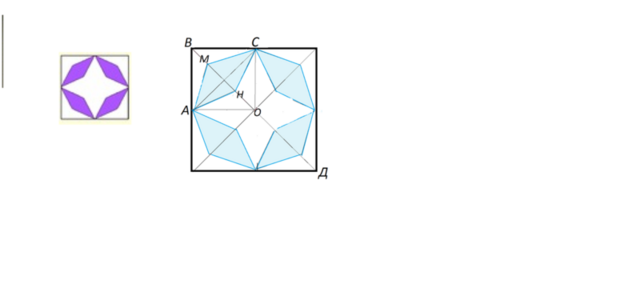
ромб АМСН на рисунке, данном во вложении.
Его вершины А и С лежат на середине сторон квадрата.
Две другие вершины М и Н лежат на диагонали ВД квадрата.
МН - меньшая диагональ ромба- по условию равна 1/6 диагонали ВД квадрата со стороной 21 ( Отрезок
МН, соединяющий вершины, расположенные на диагонали квадрата, - и
есть меньшая диагональ ромба).
По формуле диагональ
d квадрата равна d=а√2 =>
d=21√2,
следовательно, расстояние
МН=d
:6=
(21√2):6 см
АС - диагональ квадрата АВСО, сторона которого равна половине стороны исходного квадрата.
АВ=21
:2=
10,5см
АС=
10,5√2 ( опять же по формуле диагонали квадрата
d=а√2)
Площадь ромба равна половине произведения его диагоналей.
S АМСН=АС*МН
:2={(10,5√2)*(21√2):6}:2=10,5*2*21:12=
21*21:12см²
Закрашенная часть состоит из 4-х таких ромбов.
Её площадь равна
S=4*21*21:12=4*3*7*21:12=7*21=
147см²
Сумма цифр числа 147=12.