Сторона равностороннего треугольника равна 3. определите расстояние от его плоскости до...

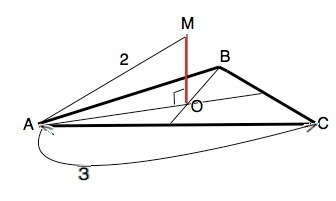
Расстояние от точки до плоскости равно длине отрезка, проведенного перпендикулярно от точки к плоскости.

Обозначим треугольник АВС, искомое расстояние МО,

Так как расстояния от М до вершин треугольника равны, т.О - центр треугольника АВС и центр описанной около него окружности, в которой АО - радиус.

Формула радиуса описанной окружности $R= \frac{a}{ \sqrt{3}}$ ⇒

R=3/√3=√3

АO=√3

∆ АМО - прямоугольный.

По т.Пифагора

МО=√(AM²-AO²)=√(4-3)=1 - это ответ.