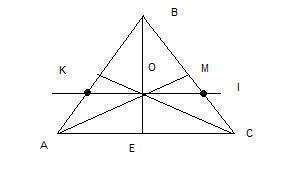
Требуется найти КМ
1. Зная, что медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2 : 1, считая от вершины, находим длину ВЕ:
ВЕ = ВО * 3 / 2 = 36 см, и ОЕ = 36 - 24 = 12 см
2. Рассмотрим треугольник АОЕ. Он прямоугольный, т.к. медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой. По теореме Пифагора найдем неизвестный катет АЕ, зная ОЕ и АО:
АЕ = √(9√2)² - 12² = √18 = 3√2
3. Получившиеся прямоугольные треугольники АЕВ и КОВ - подобные по первому признаку подобия (угол КОВ = АЕВ = 90°, угол АВЕ - общий). Значит:
 =
=  , КО =
, КО =  ;КО =
;КО =  = 2√2
= 2√2
Поскольку ВЕ - медиана, то КМ = КО*2; КМ = 2*2√2 = 4√2 см