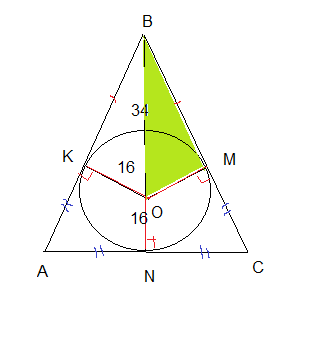Дано :Δ АВС, АВ=ВС. О-центр вписанной окружности. ВО=34, ОN=16 см.
OK=OM=ON=16 - радиусы вписанной окружности.
Стороны треугольника являются касательными к окружности.
По свойству касательной, проведенной из одной точки к окружности, отрезки касательных равны:
ВК=ВМ=30 по теореме Пифагора из прямоугольного треугольника ОВМ:
ВМ²=ОВ²-ОМ²=34²-16²=(34-16)(34+16)=18·50=900=30²
АК=АN=CM=CN=x
Так как треугольник равнобедренный и BN=(34+16)=50 cм - высота и медиана и биссектриса.
По теореме Пифагора из треугольника АВN:
AB²=BN²+AN²
(30+x)²=50²+x²,
900+60х+х²=2500+х²,
60х=1600.
6х=160,
х=80/3
S(ΔABC)=1/2 ·2x·50=50x=50·80/3=4000/3 кв.см