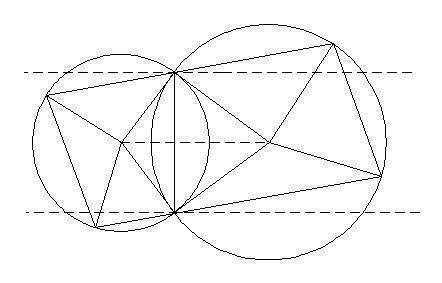
Указанные прямые пересекают каждую окружность в 4 точках
эти 4 точки образуют трапецию, вписанную в окружность.
так как окружностей две то трапеций две
в окружность можно вписать только 4-угольник, у которого сумма противоположных углов равна 180, таким каждая трапеция равнобокая.
сумма углов двух трапеций в точке пересечения окружностей равна 180, значит углы у трапеций попарно равны
значит искомая фигура (четырехугольник) образована двумя равнобокими трапециями с одинаковыми углами
значит у искомой фигуры противоположные углы равны
четырехугольник с равными противоположными углами называется паралелограммом
Доказано !