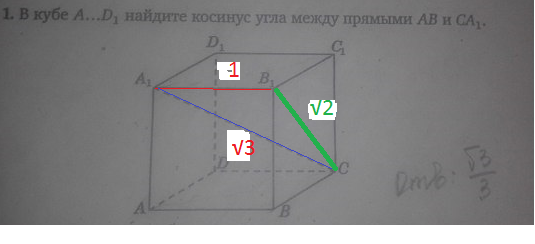
Пусть ребро куба равно 1
Диагонали боковых граней и основания по теореме Пифагора равны √(1+1) = √2
АС=√2 и В₁С=√2
А₁С по теореме Пифагора из треугольника А₁АС:
А₁С² = 1+(√2)²=3 ⇒ А₁С = √3
Угол между АВ и А₁С равен углу между А₁В₁ и А₁С , так как А₁В₁ || AB
Треугольник А₁В₁ С - прямоугольный (В₁С ⊥ А₁В₁), так как А₁В₁ ⊥ пл.(ВВ₁С₁С), а значит и любой прямой, лежащей в этой плоскости.
Косинус острого угла равен отношению противолежащего катета к гипотенузе.
сos α = A₁B₁/A₁C=1/√3=√3/3