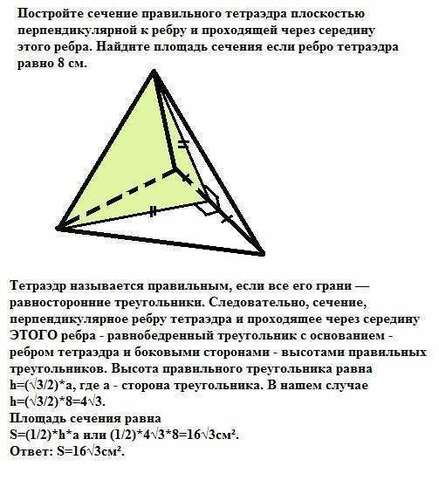
Тетраэдр называется правильным, если все его грани — равносторонние треугольники. Следовательно, сечение, перпендикулярное ребру тетраэдра и проходящее через середину ЭТОГО ребра - равнобедренный треугольник с основанием - ребром тетраэдра и боковыми сторонами - высотами правильных треугольников. Высота правильного треугольника равна
h=(√3/2)*a, где а - сторона треугольника. В нашем случае
h=(√3/2)*8=4√3.
Площадь сечения равна
S=(1/2)*h*a или (1/2)*4√3*8=16√3см².
Ответ: S=16√3см².